I have heard it said many times that SketchUp is a surface modeler. This is technically correct, but it is limited to only one type of surface: a plane. When it comes to non-planar surfaces, these must be approximated by a sufficient number of flat faces. Mathematically speaking, there are a number of other types of surfaces that are native to most surface modeling software … for example, a ruled surface:

Most people think of it as two rails connected with straight lines (or rules) proportionally spaced along the rails.
A ruled surface is not limited to having lines as the rails. Cylinders and cones are but two examples of ruled surfaces using circles or ellipses as the rails. Unlike SketchUp, however, they are infinitely continuous along the rails (i.e., no discrete points or facets):

Another common surface is the surface of revolution:
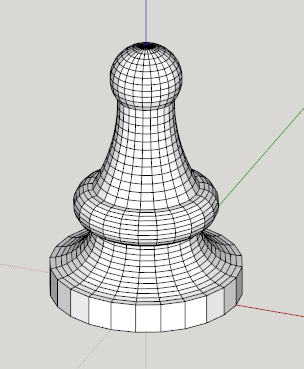
Or an extrusion along a path:
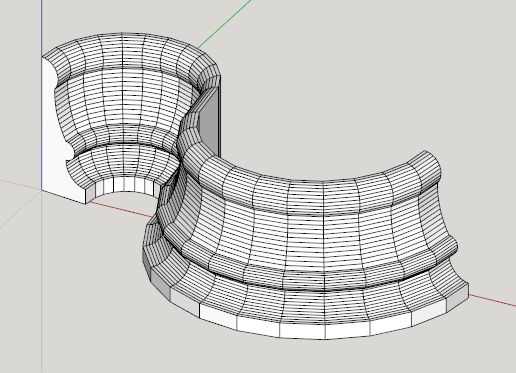
A ruled surface can be created with splines as the rails:

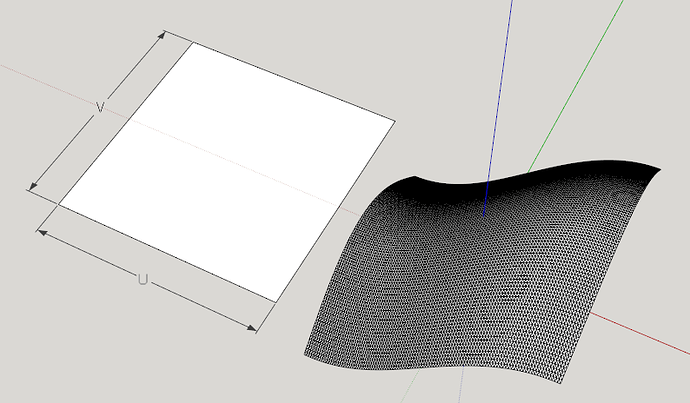
But a series of splines can also be connected at right angles to each other with another set of splines to create a Bezier surface. In a typical surface modeler, these surfaces are all stored as two dimensional planes in UV space with corresponding mapping functions to XYZ space. For example:
This is an example of a UV square defined as U from -pi/2 to pi/2 and V from -pi/2 to pi/2. For every 2D coordinate in UV space, there is a corresponding point in XYZ space given by the transformation equations:
X = U
Y = V
Z = sin(U) + cos(V)
While this can be represented in SketchUp with many small facets (20,000 triangular facets are shown in the example), a true surface modeler would continuously be able to determine any XYZ point for any given UV point and only generate discrete polygons for display purposes.
The fly in the ointment comes when trying to determine the intersection of two dissimilar surfaces. For example, a cone and a sphere:
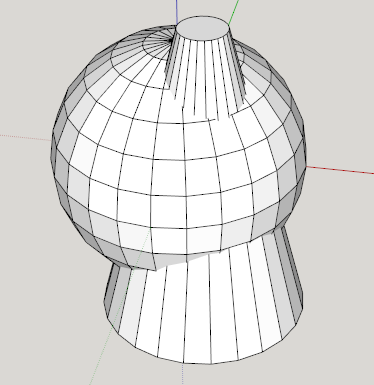
While both of these are planar in UV space, they have two different sets of mapping functions. In order to determine the intersection of the two surfaces, one must perform an iterative gradient search within the confines of the two disparate UV spaces to determine the set of XYZ coordinates common to both (usually expressed as a Bezier curve of some sort).
While some of the simpler situations have been resolved to direct solutions, the general cases usually require an inordinate amount of computational resources. It is worth noting that the intersection of two planes in XYZ space is directly solvable for a line of intersection (if it exists). Further, since faces and their bounding edges are easily represented in XYZ space as 2D items and an orientation vector, planar operations entirely within XYZ space is very computationally efficient and also integrates directly with most modern graphic display adapters. This allows SketchUp to create and display relatively complicated geometry very quickly and smoothly.
The effect of the faceted approach to modeling has been somewhat obscured within SketchUp by the addition of visual smoothing algorithms. The same shape, both smoothed and un-smoothed, renders appropriately in most engines:

With the advent of 3D printing, the underlying facets of SketchUp have become a concern when one desires a smooth print. By being aware of the limitations of facet modeling, as well as the limitations of various print media, SketchUp can produce very acceptable results if this is taken into account while creating the geometry. However, increasing the number of facets or points on a curve may not necessarily be easily achievable after the fact.
This is one of the main distinctions and advantages of a true surface modeler as any decisions regarding surface smoothness can be delayed until the final design is completed. Only when it is time to export it for 3D printing or CNC machining does some sort of surface (or curve) approximation tolerance need to be specified.