Dimension Calculation Problem | Finally Cornered!

Technical Problems SketchUp
,
21

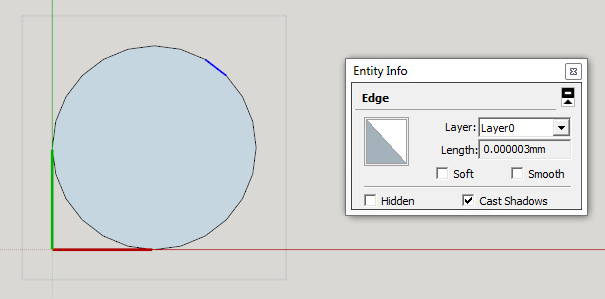
The minimum tolerance doesn’t matter. In an output for CNC it doesn’t matter if a redundant point is .00001" from the other point or .0001". It’s still a redundant point that creates errors. Or if you push/pull a plane all the way through. If you’re object is .720000" thick and it only pushes .719999…it’s not going all the way through. The difference between existence and non-existence. It’s pretty huge. I’m now redrawing 2 days worth of work for these crazy complex doors.

Also speaking from the perspective of someone that does CNC commercially. It triples the amount of time when some one drops off an erroneous file that requires hours or redrawing (often from scratch). I usually charge a lot for that or turn them away.

SketchUp for fantasy is one thing, but if you’re actually making things and you’re in a workflow with other people and other software you have to be extremely meticulous.

1 Like
22

Woah. I found it! I went around measuring every last plywood plane. I found one from earlier in the modeling that was .720002. I redrew it with proper dimensions. I’m not having the problem anymore. I think that all the new planes were inheriting these messed up dimensions via the snapping feature. Seems to be gone for now.

3 Likes
23

Indeed, once dimensional inaccuracies get created, they tend to be propagated as the user relies on SketchUp’s faithful inference engine. The key is to prevent inaccuracies in the first place, or to notice them and correct them as soon as possible.

I don’t think SketchUp has flat-out bugs which cause sloppy calculation results (at leasts I’ve never encountered such a thing, and I’ve been something of a personal perfectionist for a few years in SketchUp). Inaccuracies can be unintentionally introduced when not quite letting SketchUp settle on an inference point, instead clicking right nearby what is expected to be an inference point. I do that occasionally.

One tip: if you hover the mouse over a well-defined location and wait for SketchUp to display a little tool-tip that describes the location (e.g., “Endpoint” or “Center” or “Origin”) which takes about a second or so, then the inference engine will recognize and utilize that point. If instead you move the mouse very close to the intended location but don’t hover for a second to let SketchUp display the tool-tip, the inference engine may not lock on and instead a mouse-click will perform the action where the mouse was pointing - a bit off of the intent.

24

It’s not a matter of the type of units used, but the dynamic range covered and the use of floating point binary numbers in the calculations. A unit cube is one unit in each dimension, regardless of whether it’s in millimeters or leagues. In the case of SketchUp, if you want the units in inches, multiply them by 1. If you want them in millimeters, multiply them by 25.4. Internally, somewhere, it’s only a number relative to other numbers … humans assign a name to the units, not the geometry itself.

Using the “Dave Method”, you can scale things down pretty far. A 1" square can be shrunk to a 0.000001" square:

image

“Circles” behave similarly:

image

Talk about your tiny edges, here’s one that’s zero in length:

image

However, if I switch the model units to millimeters:

image

Some decimal (base 10) numbers just don’t work out in binary (base 2). Binary integers are pure, but binary representation of decimal fractions is not. 1/4 can be exactly represented in binary as 0.01, but 1/3 cannot. Some decimal-to-binary-to-decimal calculations transform 1.0 into 0.9999999999999, which can introduce unwanted errors. In a former life, I had FORTRAN computer that utilized 128-bit floating-point for a CAD application; even then, I would sometimes encounter approximation issues.

If we were intended to use binary for our calculations, why were we born with ten digits on our hands instead of only two?

I tried to model the Solar System and discovered that the range of values wasn’t big enough to make planet-sized spheres and place them 4.5 billion kilometers apart. I ended up scaling everything down by 400,000,000:1:

The Universe would require a much larger scale factor :wink:

3 Likes